Collaborative Filtering: From Shallow to Deep Learning

Collaborative filtering is commonly used to create recommender systems (e.g., Netflix show/movie recommendations). The current state-of-the-art collaborative filtering models actually use quite a simple method, which turns out to work pretty well. In this post I will give an overview of these state-of-the-art models, which utilize “shallow learning,” and then introduce a newer method (in my opinion promising!), which utilizes deep learning. Within this post I will use the MovieLens dataset as an example, which contains users’ ratings of movies. I also demonstrate how to use shallow and deep collaborative filtering in the script provided on my Github, so if you would like to use these models, check out my Github! This script makes use of the excellent deep learning library fastai (which is written on top of PyTorch) and PyTorch.
Shallow Learning
The current most popular collaborative filtering models make use of something called embedding matrices. Embedding matrices contain multidimensional information. For example, lets say we have an embedding matrix for movies with three factors. It may be the case that these three factors correspond to how action pact the movie is, how romantic is the movie, and if the movie is more similar to a documentary or not. Of course, these factors could correspond to anything (and are not necessarily easy to interpret) and embedding matricies often contain many factors. It is these matrices that are updated when training a collaborative filtering model. Using the MovieLens dataset example, with our standard collaborative filtering technique we would have an embedding matrix for the users and the movies (see the figure below). The size of the matrix would be the number of users or movies by the number of factors we choose. In regards to choosing the number of factors in the embedding matrices, that requires some trial-and-error. In the example script on my Github, the number of embedding factors was set to 50. Before the start of training, the values within these embedding matrices are randomly initialized. During training, these values are updated in service of reducing the loss (i.e., making the predicted ratings more similar to the actual ratings). During each iteration of training, for each user’s rating of a movie, the dot product of the corresponding vectors are taken. This dot product is the predicted rating. The dot product is taken for every single user’s rating of every movie rated (Note: movies that were not rated by a movie are set to 0), and the predicted ratings are compared to the actual ratings. Then, stochastic gradient descent (or close variants of stochastic gradient descent) are used to update the values within the embedding matrices in service of reducing the loss function. In addition to the embedding matrices, state-of-the-art collaborative filtering models contain a bias term, which is essentially to account for certain users that always give either more high or low ratings or movies that overall are given more high or low ratings (i.e., good or bad movies). These bias terms are added to the dot product.

And that really all there is to a state-of-the-art collaborative filtering model. As you can see, the math behind all of this is quite simple, and if you take a look at the accompanying script posted on my Github, you’ll see that with the use of the fastai library, creating and training a state-of-the-art collaborative filtering model can be achieved with only a few lines of code.
Deep Learning
Okay so we’ve covered the current state-of-the-art collaborative filtering model, which works quite well and makes use of “shallow learning”, but what’s next for the field? Well a promising direction may be collaborative filtering with deep learning because (1) deep learning has been extremely successful in other lines of work (e.g., computer vision) and (2) it allows for greater model specifications, which at first sounds really annoying, but may allow machine learning practitioners to create models that are tailored to their datasets. The idea of collaborative filtering with deep learning, to my knowledge, was first presented within the fastai MOOC, and I think it’s a very exciting direction for the field! Before going into the details of collaborative filtering with deep learning, I have to admit that using the example MovieLens dataset the shallow learning model outperformed the deep learning model. However, I think with enough modifying the architecture of the model and with the right dataset (maybe larger datasets — I was using only a subsection of the MovieLens dataset), collaborative filtering with deep learning can outperform shallow learning models.
Here, I am going to go over a model with only one hidden layer, but these models can be customized in any way you want! Note: I did try adding more layers and with this dataset the one hidden layer model performed the best.
Just like before, we start off by creating an embedding matrix for the movies and users with randomly initialized weights (size is the number of users or movies by the specified number of factors). Then, for each user and the corresponding movie embedding factor vectors, we concatenate these vectors (see below in the figure). In the example script, there is a little bit of drop out at this point (0.05) to prevent overfitting. Then, we multiply the concatenated embedding factor vector by another matrix with a size of embedding factors*2 (in this example, it has to be this since this is the number of columns in the concatenated embedding vector) by some other number (in the example I have 10). The matrix product is then put through a rectified linear units activation function (ReLU; this is a fancy way of saying that the negative values were changed to 0); this is very common in deep learning and makes the function non-linear. Again, to prevent overfitting, we apply more dropout. Afterwards, we take the matrix product (which went through ReLU and dropout) and multiply it by a matrix that has some other number of rows (again, in this example 10) and one column. Therefore, the output of the matrix multiplication will be one number, which is exactly what we want since we are trying to predict one rating. This predicted rating is then put through a sigmoid function (multiplied by [(Maximum Rating — Minimum Rating) + Minimum Rating]) in order to make the predicted value closer to actual predictions in the dataset. This is repeated for everything single user and rating, and just like before, the predicted values are compared to the actual values, and the values within our model are updated with stochastic gradient descent with backpropagation (just like with any deep learning problem).
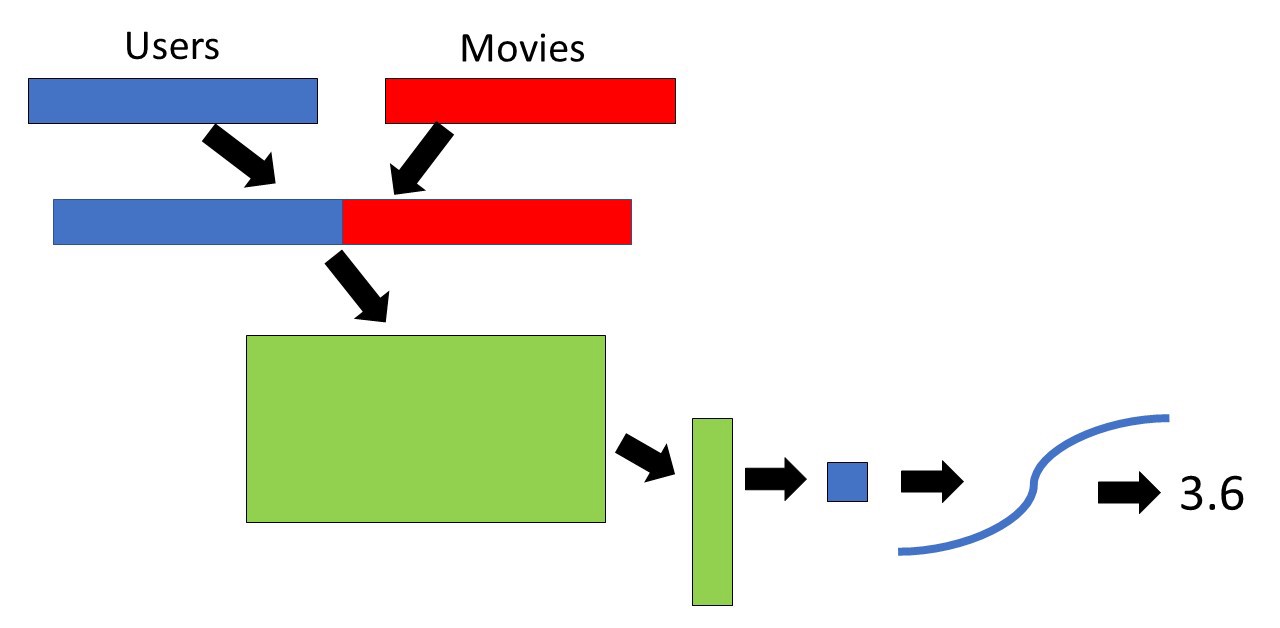
Something to note here is that I have not mentioned anything about bias and that is because the linear layers within PyTorch already take into account bias, so we don’t have to worry about it.
Again, as I mentioned before, the deep learning model did worse than the shallow learning model, but I believe this framework is a promising line of work. If you would like to try out the example mentioned in this post, check out my Github. I look forward to hearing readers’ comments and perhaps seeing other uses of collaborative filtering with deep learning.